
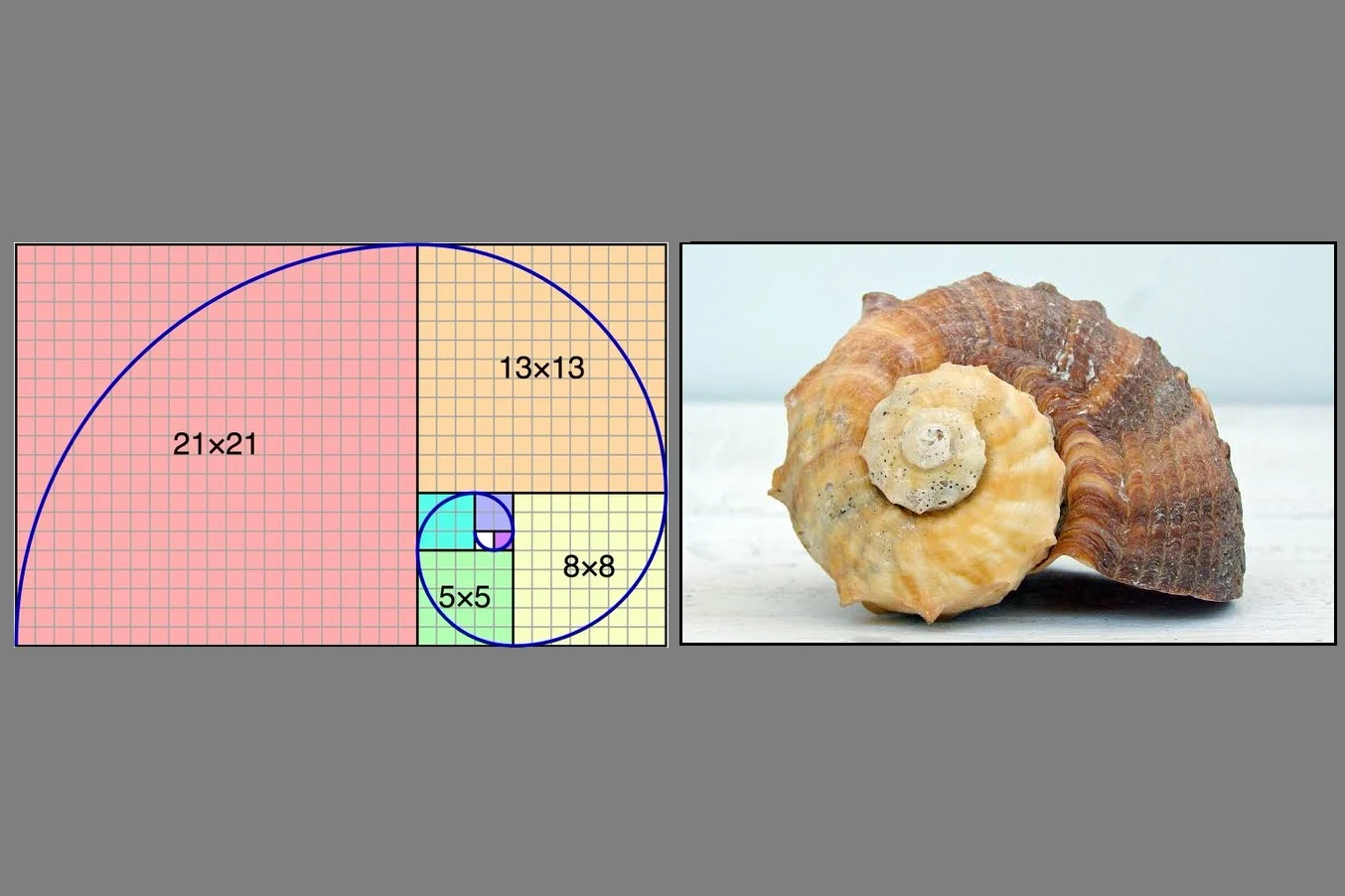
It is usually denoted by the Greek letter \(\varphi\) ( phi), and sometimes by \(\mu\) ( mu). This number was known to the ancient Greeks and was called by them the golden mean. (It is not rational, so the actual decimal doesn’t repeat or terminate.) This is a simple equation to solve for \(x\): it is really a quadratic equation, and its positive root is the value we are looking for: \Ĭonsequently, the real number \(x\) to which the sequence of ratios converges must satisfy the following equation: This is an example of a recursive sequence, obeying the simple rule that to calculate the next term one simply sums the preceding two: After this things expand rapidly, and we get the following sequence of numbers: In the fourth month 3 pairs will be produced, and in the fifth month 5 pairs. It is easy to see that 1 pair will be produced the first month, and 1 pair also in the second month (since the new pair produced in the first month is not yet mature), and in the third month 2 pairs will be produced, one by the original pair and one by the pair which was produced in the first month. How many pairs of rabbits will be produced in a year, beginning with a single pair, if in every month each pair bears a new pair which becomes productive from the second month on? Medieval mathematician and businessman Fibonacci (Leonardo of Pisa) posed the following problem in his treatise Liber Abaci (pub. Zeno’s Paradox of the Tortoise and Achilles.


 0 kommentar(er)
0 kommentar(er)
